今回で論理と集合は最終回です。最後まで頑張っていきましょう！

―対偶を利用した証明法―

　まずある命題pに対して、その否定をで表します。たとえば「xは奇数である」の否定は、「xは偶数である」となります。そして、命題p⇒qに対してq⇒pを逆、 を裏、 を対偶といいます。

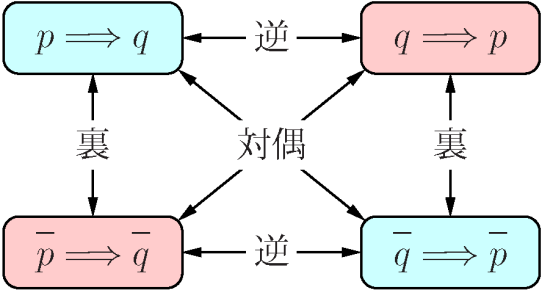
　ある命題が真であっても、その命題の逆が真であるとは限りません。これは必要条件、十分条件のところでお話ししましたね。しかし、元の命題の真偽とその対偶の真偽は必ず一致します。これを利用してもとの命題が真であることを証明する方法があります。

例1　x+y+z≧0のとき、x,y,zの少なくとも1つは0以上であることを証明しなさい。

解答

「x,y,zの少なくとも1つは0以上である」の否定は，「x,y,zがすべて0より小さい」

この命題の対偶は

x,y,z<0　ならば　x+y+z<0

となる。対偶が真であるから，もとの命題も真である。

例2　nが自然数を表す時，n²が奇数ならば，nは奇数であることを証明しなさい。

解答

この命題の対偶は

nが偶数ならば、n²は偶数である。

である。ここでnをある自然数kを用いて、n=2kと仮定すると、

n²=4k²=2(2k²)

は偶数になる。対偶が真であるから、もとの命題も真である。

―背理法を利用した証明法―

ある命題を証明するために、その命題が成り立たないと仮定すると矛盾が導かれることを示し、そのことによってもとの命題が成り立つと結論する方法が用いられる。この証明法を背理法といいます。具体的には…

例 　自然数a,b,cについて、a²＋b²＝c²が成り立つとき、a,b,cのうち少なくとも１つは偶数であることを証明しなさい．

解答

a²＋b²＝c²　　　①

ここで、「a,b,cは奇数である(②)」と仮定する。

②より左辺について

(左辺)=a²＋b²

=(奇数)＋(奇数)

=(偶数)

となります。一方、右辺について

                                                        (右辺)= c²=(奇数)

となります。これらを合わせると

(左辺)≠(右辺)

となり矛盾します。

これよりa,b,cのうち少なくとも１つは偶数であるといえます。

…とこのように、何かを仮定したときに矛盾が生じることからその仮定が間違っていると証明するのが背理法です。「…でないことを証明しなさい。」や「少なくとも…であることを証明しなさい。」といったことを証明するときに背理法を用いることが多いです。

この記事で扱った例題の解答はそっくりそのまま覚えて、自分で書けるようになりましょう。書き方はだいたいどの問題でも同じです。(背理法は慣れるまでちょっと難しいかも。。。)自分で書けるようになったらOKです！

Part1 : https://www.ikstudie.com/articles/183
Part2 : https://www.ikstudie.com/articles/186
Part3 : https://www.ikstudie.com/articles/192
Part4 : https://www.ikstudie.com/articles/193